Dentro del núcleo estructurante «Operaciones» uno de los saberes básicos fundamentales que se ha observado tienen dificultades los alumnos es respecto a resolver problemas y operar en el conjunto de los números racionales.
Este saber básico está incluido en los saberes que se proponen promover desde los Núcleos de Aprendizajes Prioritarios de séptimo grado, en Relación con el Número y las Operaciones, en donde se puntualiza:
El reconocimiento y uso de las operaciones entre números naturales, fracciones y expresiones decimales y la explicitación de sus propiedades en situaciones problemáticas que requieran:
- operar con cantidades y números seleccionando el tipo de cálculo (mental y escrito, exacto y aproximado, con y sin uso de la calculadora) y la forma de expresar los números involucrados que resulte más conveniente en función de la situación, y evaluando la razonabilidad del resultado obtenido
- producir cálculos que combinen varias operaciones en relación con un problema y un problema en relación con un cálculo, y resolverlos con o sin uso de la calculadora
- argumentar sobre la validez de un procedimiento o el resultado de un cálculo mediante las propiedades de la suma, la resta, la multiplicación y la división.
A continuación se muestran algunos ítems de evaluación que obtuvieron en general menos del 50% de respuestas correctas. Por ejemplo en la evaluación de 2013 el ítem correspondiente a este saber obtuvo un 45,28% de aciertos.
Los ejercicios dados corresponden a varios operativos de evaluación (provinciales, nacionales e internacionales) porque en ellos, a pesar de ser poblaciones distintas y de distintos años, los alumnos repiten los mismos errores.
Es importante recordar que cada uno de los distractores que aparecen NO han sido puestos al azar, son posibles formas de razonar que tienen los alumnos, o un aprendizaje incompleto que en algunos casos les resulta válido. Por ello en evaluación sistemática se los llama «distractores válidos», al elegirlos queda claro el error que tienen los alumnos.
| [1] |
Juan, Pedro Luis y José salieron hacia el club. Algunos se pararon a descansar en el camino. Juan iba en bicicleta. Pedro en moto. Luis corriendo y José caminando.
Juan recorrió— ![]() del camino; Pedro
del camino; Pedro ![]() ; Luis
; Luis ![]() y José
y José ![]() del camino. ¿Quién está más cerca del club?
del camino. ¿Quién está más cerca del club?
- Pedro
- Juan
- José
- Luis
[2]
En un grupo de niños, 16 cumplen años durante la primera mitad del año y los 14 restantes cumplen años durante la segunda mitad del año. ¿Qué fracción del grupo cumple años durante la primera mitad del año?. Considera al año con 12 meses.
[3]
A Mario le regalaron 3 láminas de fútbol, 4 láminas de autitos y 2 láminas de animales. ¿Qué fracción representan las láminas de fútbol del total de láminas?
[4]
Lee atentamente:
En un barrio de 30 casas, ![]() de las casas tienen calefón. Esto quiere decir que:
de las casas tienen calefón. Esto quiere decir que:
- 14 casas tienen calefón y 30 casas no lo tienen.
- 14 casas tienen calefón y 16 casas no lo tienen.
- 16 casas tienen calefón y 14 casas no lo tienen.
| [5] ¿Cómo se calculan los 2/5 de 120?
|
[6] En una bolsa hay bolitas de cristal y de piedra. Si |
Cuando los niños comienzan a abordar el estudio sistemático de las fracciones en la escuela, tienen ya una amplia experiencia con los números naturales. Esa experiencia será para ellos el punto de apoyo a partir del cual extenderán progresivamente el campo numérico, pero al mismo tiempo se constituirá en el mayor obstáculo frente al desafío de comprender el funcionamiento de estos nuevos números. ¿Qué nos lleva a hacer una afirmación tan drástica? El aprendizaje de los números racionales –escritos en forma decimal o fraccionaria– supone una ruptura fundamental con lo que el niño sabe hasta el momento: los números ya no tienen siguiente, la multiplicación no puede –salvo cuando se multiplica un natural por una fracción– ser interpretada como una adición reiterada, en muchos casos el producto de dos números es menor que cada uno de los factores, el resultado de una división puede ser mayor que el dividiendo, un número –la fracción– se representa a través de dos números naturales. En fin, un edificio de certezas construido durante años, parece derrumbarse.
Al abordar las fracciones, la idea de “parte” no siempre está vinculada explícitamente con la división. Apoyarse en los conocimientos que los niños tienen sobre ella permite iniciar el trabajo con fracciones y ligarlas al resultado exacto de una división entre números naturales, presentando situaciones en las que las fracciones expresan el resultado de un reparto; por ejemplo, cuando 4 niños deciden compartir 3 chocolates. Esto también permite trabajar a la vez con fracciones mayores que uno.
Tal como ocurre con cualquier noción matemática, el sentido de la noción de número racional se construye a partir de los problemas que van enfrentando los alumnos y que no pueden ser resueltos usando los números naturales.
La enseñanza de las fracciones es una de las tareas más difíciles en la educación general básica. Dicha dificultad se manifiesta en el alto porcentaje de niños que fracasan en aprender este contenido.
Los números fraccionarios son una estructura de una riqueza y complejidad que encuentra aplicaciones en una multiplicidad de contextos: la ciencia, la técnica, el arte y la vida cotidiana. En cada uno de estos contextos las fracciones se presentan con una diversidad de significados.
Uno de los aspectos que determinan el fracaso es la falta de tratamientos de los diferentes campos conceptualesrelativos al objeto matemático fracción.
Campo conceptual es un espacio de problemas, cuyo tratamiento implica conceptos y procedimientos de varios tipos en estrecha conexión entre sí. El espacio de problemas correspondiente a un campo conceptual está dado por el tipo de operaciones o de relaciones que demanda.
La construcción y la comprensión de un campo conceptual es un proceso complejo, que se extiende durante un largo período, produciéndose en esta construcción aproximaciones sucesivas al concepto. Según algunos autores como Sallán (2005) se deben tener en cuenta cinco significados de la fracción:
- La fracción como relación parte-todo. La interpretación de las fracciones como relación parte-todo se produce cuando un todo (continuo o discreto) se divide en partes iguales.
Por ejemplo, en un envase de 12 huevos hay 5 que están cascados. ¿Qué fracción de huevos del envase está cascada? ¿Qué fracción de huevos del envase no está cascada?
- La fracción como cociente. En la interpretación de las fracciones como cociente se asocia la fracción a la operación de dividir un número natural por otro.
Por ejemplo, ![]() podría representar la acción de dividir 3 litros entre 5 personas.
podría representar la acción de dividir 3 litros entre 5 personas.
- La fracción como razón. En la interpretación de las fracciones como razón, la fracción aparece como razón de una proporción.
Por ejemplo, la razón como escala, en una comparación de longitudes.
- La fracción como operador. En el caso de la fracción como operador, la fracción actúa como transformación, como función. El conjunto original puede ser un conjunto numérico o una magnitud.
Por ejemplo, si de 20 alumnos, ![]() aprobaron el examen de ciencias. ¿Cuántos alumnos no aprobaron?
aprobaron el examen de ciencias. ¿Cuántos alumnos no aprobaron?
Tomemos algunos ejemplos de tipos de problemas que le dan sentido a las fracciones. En primer lugar analicemos los problemas de reparto, en los que tiene sentido indagar una situación de partes equitativas, los cuales pueden dar lugar a una diversidad de procedimientos.
Los niños pueden recurrir a distintas formas de repartir y distribuir porciones y discutir acerca de la noción de equivalencia de las partes. Por ejemplo:
En una mesa de un bar se sientan 4 personas y piden, para compartir, tres pizzas chicas. En otra mesa, piden 4 pizzas chicas pero son 5 comensales. ¿En qué mesa come más cada persona?
Esto también puede dar lugar a considerar la relación entre las pizzas repartidas y el número de comensales, así como el tamaño y número de las partes. Más adelante, esta reflexión será un punto de apoyo para interpretar ![]() como el resultado del cociente entre el número a y el número b.
como el resultado del cociente entre el número a y el número b.
Para el caso de las expresiones fraccionarias, es frecuente que el trabajo comience usando la idea de partes de un todo dividido en porciones iguales: esto permite abordar las relaciones entre el tamaño y el número de las partes con fracciones menores que uno; pasar luego a la suma y a la resta con fracciones del mismo denominador y, después, a las de distinto denominador.
En los problemas en contextos de medida esta progresión es prescindible, ya que el uso de equivalencias y de estrategias de cálculo mental permite resolver, sin conocer los algoritmos para operar con fracciones de distinto denominador.
Por ejemplo es posible calcular ![]() , pensando que
, pensando que ![]() equivale a
equivale a ![]() ; o a 3 veces
; o a 3 veces ![]() , y que
, y que ![]() litro son dos cuartos litros, teniendo control sobre el resultado. Es más, incluso se pueden presentar problemas que involucran distintas operaciones y/o diferentes significados de las mismas, con el objeto de analizar los límites de la utilización de cada una de ellas.
litro son dos cuartos litros, teniendo control sobre el resultado. Es más, incluso se pueden presentar problemas que involucran distintas operaciones y/o diferentes significados de las mismas, con el objeto de analizar los límites de la utilización de cada una de ellas.
Otro problema en el contexto de la medida puede ser el siguiente:
- En una panadería quedaron 4 bolsas de
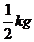 de pan y 9 bolsitas de
de pan y 9 bolsitas de 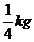 .El pan que sobra es envasado en bolsas de 5 kg para secar y usar en otras preparaciones. ¿Alcanza con lo que tienen o necesitan más para llenar una bolsa de 5 kg?
.El pan que sobra es envasado en bolsas de 5 kg para secar y usar en otras preparaciones. ¿Alcanza con lo que tienen o necesitan más para llenar una bolsa de 5 kg? - Otro día, habían quedado del día anterior 7 bolsas de
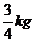 , ¿les alcanza para completar los 5 kg?
, ¿les alcanza para completar los 5 kg? - El ayudante que arma las bolsas tiene una bolsa de
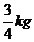 , otra de
, otra de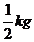 , otra de 1 kg y una chiquita de
, otra de 1 kg y una chiquita de 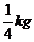 . ¿Cuánto le falta para completar los 5 kilos?
. ¿Cuánto le falta para completar los 5 kilos?
En estos casos, es posible resolver apoyándose en la suma, y retomar un significado de la multiplicación con el que los alumnos ya están familiarizados, para ir construyendo los primeros procedimientos de cálculo de dobles o mitades, triples, entre otros.
También habrá que considerar situaciones de partición en las que, dado el valor de cada parte es necesario averiguar la cantidad de partes en las que puede subdividirse el total; como, por ejemplo, cuando hay que determinar cuántas botellas de ![]() pueden llenarse con 5 litros. Otro ejemplo podría ser:
pueden llenarse con 5 litros. Otro ejemplo podría ser:
En un almacén se vende aceite que viene en bidones de 5 litros, fraccionándolo en botellas de ![]() . ¿Cuántas botellas se deberán utilizar por cada bidón?
. ¿Cuántas botellas se deberán utilizar por cada bidón?
También es posible presentar varias preguntas que requieran considerar nuevas fracciones y expresiones decimales. Por ejemplo:
En un establecimiento en el que producen aceite de oliva hay un tanque con 35 litros de aceite. Para su venta, se decide usar distintos envases. ¿Cuántos son necesarios para envasar esa cantidad de aceite si usan envases de ![]() , de
, de ![]() , de
, de![]() o de 0,2 litro?
o de 0,2 litro?
Resulta interesante considerar con los alumnos qué cálculos conviene realizar antes que otros, para apoyarse en los resultados obtenidos, lo que permite explicitar relaciones entre fracciones o entre fracciones y expresiones decimales.
La ampliación del trabajo sobre la medida, con actividades que requieran medir o construir segmentos, y con propuestas en las que haya que trabajar sobre la recta numérica, y el estudio de situaciones en las que las fracciones expresen constantes de proporcionalidad, permitirá ir conociendo la multiplicidad de significados del número racional. Dado que estos significados no pueden ser abordados al mismo tiempo, será importante articular el tratamiento de los mismos en los distintos grados de la escuela.
Pueden ser propuestas actividades que involucran mediciones de longitudes y de áreas, en las que la cantidad elegida como unidad no esté contenida un número entero de veces en la cantidad a medir, lo que lleva a explicitar la insuficiencia de los números naturales para expresar los resultados. Por ejemplo:
Si el segmento AB es la unidad que se usa para medir, ¿cuál es la medida de CD y de MN?
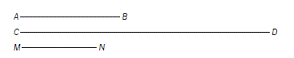
Dibujar segmentos cuyas medidas resulten:
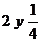 de AB
de AB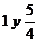 de AB
de AB
Dibujar el segmento unidad, sabiendo que el segmento BC mide ![]() de la unidad.
de la unidad.
![]()
Dibujar el segmento unidad, sabiendo que el segmento BC mide ![]() de la unidad.
de la unidad.
![]()
Marcar en la recta numérica ![]() ,
,![]() ,
,![]() ,
,![]() ,
, ![]()
![]()
¿A qué número corresponde A? ¿y B y C?
![]()
Al resolver estos problemas los alumnos suelen medir con la regla, sin tener en cuenta que, en algunos casos, es posible obtener la unidad repitiendo la parte conocida como dato, y sin conocer su longitud.
Al trabajar con actividades donde lo pedido es representar en la recta numérica, hay que tener en cuenta si la longitud del segmento unidad (ya sea en cm o en ‘cuadraditos’, en caso de usar papel cuadriculado) es o no múltiplo de los denominadores de las fracciones que se quiere representar, y si están dadas las posiciones del 0 y el 1, ó del 0 y otro número, ya que la dificultad podría ser muy distinta en un caso u otro.
A propósito de las pizzas y de las tortas, es usual que la escuela adopte el modelo de partir pizzas y tortas para “presentar” el concepto de fracción. Tan natural resulta esta opción que muchas veces el modelo suele confundirse con el concepto mismo, sin que se tenga demasiada conciencia de la cantidad de puntos de vista vinculados al concepto de fracción que quedan afuera del esquema “partir un todo en partes iguales”. ¿Qué queremos decir con esto?
Por ejemplo, es frecuente, ante la tarea de decidir si, por ejemplo, la parte rayada del siguiente dibujo representa 1/3 de la unidad, los niños contestan que no “porque no está partida en partes iguales”. El problema de evaluar una medida se reduce entonces a una cuestión de percepción que no pone en juego el concepto de fracción.
![]()
Este ejemplo muestra algunos inconvenientes que surgen al identificar el concepto de fracción con la subdivisión real del todo en partes iguales.
Estos inconvenientes se ponen también de manifiesto frente a la tarea de medir un objeto mayor que una unidad.
Las consideraciones anteriores no intentan ser una prédica contra el recurso de utilizar tortas y pizzas para enseñar fracciones, apuntan más bien, a identificar cuáles son los aspectos que esta presentación no aborda y, por lo tanto, a señalar las limitaciones que surgen cuando se la concibe como primer, único y excluyente modelo para la enseñanza de las fracciones.
En el apartado de propuestas de enseñanza, hay sugerencias y actividades para poder ir sorteando estos obstáculos.



