Los errores recurrentes evidenciados en nuestros alumnos por el bajo porcentaje de respuestas correctas en el bloque de “Numeración” siguen teniendo sus causas en el aprendizaje del Sistema de Numeración.
Es importante remarcar que la incorporación de los números decimales y las fracciones en el segundo ciclo, implica un nuevo trabajo en la tarea docente, con la consabida complejidad que representa el aprendizaje de estos conjuntos numéricos.
Las secuencias que se presentan no están en general pensadas para que los alumnos resuelvan de manera inmediata la tarea que se les propone. Sí se espera -cada vez- que puedan empezar a abordar, explorar, ensayar. En algunos casos, podrán arribar a conclusiones de manera bastante autónoma y en otros requerirán de la ayuda del docente. Alentamos la tarea de exploración como un modo de formar a un alumno autónomo, que acepta el desafío intelectual, que elabora criterios para validar su propio trabajo.
A propósito de algunos de los problemas, es probable que los alumnos evidencien cierta dificultad para entender con precisión qué es lo que se les pide. Puede ser que el docente interprete que el alumno no comprende la consigna. Sin embargo, la falta de comprensión de la consigna se vincula en general con el hecho de que la tarea en danza es conceptualmente nueva; por eso, entender lo que se pide supone para los alumnos ampliar su perspectiva respecto de los conceptos involucrados en el problema.
En esos casos seguramente serán necesarias explicaciones del docente que “completen” la formulación escrita del problema.
Estas explicaciones son un modo de empezar a comunicar las nuevas ideas que están en juego.
Los números decimales no son un asunto nuevo para los alumnos. Sin embargo, es probable que, pasado un tiempo, se hayan olvidado de algunas relaciones con las que es interesante contar para continuar profundizando el estudio. Por esa razón proponemos una situación de repaso que permita explicitar un “piso común” a partir del cual retomar el trabajo. Será necesario recordar lo siguiente:
- la estructura posicional de la notación decimal: cada cifra representa una fracción decimal de la unidad multiplicada por el valor de esa cifra;
- las relaciones de valor entre posiciones contiguas (10 veces 0,1 es 1; 10 veces 0,01 es 0,1);
- la multiplicación por 10, 100, 1.000, …, sobre la base de las relaciones anteriores.
Repasando cuestiones básicas de los números decimales
Problemas
Seguramente el año pasado estudiaste números decimales. Puede ser que no recuerdes del todo algunos de los asuntos estudiados y, por eso, empezaremos ahora con un repaso.
- Anotá, usando fracciones y considerando el peso ($) como unidad, las siguientes cantidades de dinero, expresadas en decimales.
| Notación decimal ($) | Notación fraccionaria ($) | ||
|---|---|---|---|
| 0,50 | |||
| 0,25 | |||
| 0,10 | |||
| 2,25 | |||
| 0,05 | |||
| 3,05 | |||
| 2,80 | 2,8 |
¿Cuánto dinero (en $) hay en 10 monedas de 10 centavos? ¿Y en 10 monedas de 1 centavo? ¿Y en 100 monedas de 1 centavo? ¿Y en 100 monedas de 10 centavos? De las cuestiones anteriores surgen algunos cálculos:
0,10 x 10 = 0,01 x 100 =
0,01 x 10 = 0,1 x 100 =
- Apoyados en los cálculos anteriores, realicen ahora estos cálculos:
0,2 x 10 = 0,2 x 100 =
1,2 x 10 = 1,2 x 100 =
0,02 x 10 = 0,02 x 100 =
1,02 x 10 = 1,02 x 100 =
1,22 x 10 = 1,22 x 100 = - Ya sabés que de una multiplicación siempre se pueden extraer dos divisiones.
Por ejemplo, si se sabe que 1,2 x 10 = 12, se sabe también que 12 : 10 = 1,2; y que 12 : 1,2 = 10.
Anotá todas las divisiones que surgen del problema 3.
- Escribí reglas para multiplicar por 10 y por 100 un número decimal.
-
Es muy fácil recordar que, si se reparte $ 1 entre 10 personas, cada una recibe 0,10 y que esto “lleva” al cálculo 1 : 10 = 0,1. De la misma manera $ 1 repartido entre 100 (aunque sea raro) da 0,01, lo cual nos permite recordar el cálculo 1:100=0,01.
¿Cuánto es 0,1 : 10? Explicalo usando las relaciones anteriores.
Valor posicional
En los problemas que se proponen a continuación se analizará el valor posicional de las cifras en las escrituras decimales, las equivalencias entre las posiciones contiguas y no contiguas de la escritura decimal y las operaciones subyacentes a las escrituras decimales.
Problemas donde “vale” la calculadora
- Si sólo se pudieran apretar las teclas “0”; “1”; “.” ; “+” de la calculadora:
- ¿Cómo podrían escribirse los siguientes números? Anotá en tu carpeta la cuenta que harías.
0,2; 0,03; 0,005; 0,25; 0,375; 341,406
- Para anotar un número, Juan sumó 3 veces 0,001; 3 veces 0,1 y 4 veces 0,01. ¿Qué número anotó?
- Intentá armar 1,02 de dos maneras diferentes. ¿Y 1,2?
- ¿Qué número se arma sumando 10 veces 0,1; 10 veces 0,01 y 10 veces 0,001? Anticipalo antes de verificarlo en la calculadora.
Respondé:
-
- ¿Qué número se arma haciendo 5 x 0,1 + 3 x 0,01?
- ¿Qué números se forman haciendo los siguientes cálculos?
4 x 0,1 + 3,001 + 5 x 0,001
7 x 0,1 + 6 x 0,001
2 x 0,01 + 5 x 0,001 - Propongan cálculos similares para que rápidamente un compañero pueda dar el número e intercámbienlos.
- Resolvé los siguientes problemas:
- Si en el visor de la calculadora escriben el número 3,452, ¿qué cálculo hay que hacer en la máquina para que aparezca el número 3,402 sin borrar? ¿Y para que aparezca 3,052?
- Si en el visor de la calculadora está el número 2,347, ¿qué deben hacer para que aparezca el número 2,007 sin borrar?
- Pensando con la calculadora.
- Si anotás en la calculadora 29,8; sumás 0,1 y seguís apretando la tecla “=”, se suman 0,1 cada vez que volvés a apretar “=”. Anotá qué números irán apareciendo si apretás 5 veces la tecla “=”. Después, verificalo con la calculadora.
- ¿Y si a 29, 8 le sumás 0,01?
- Si a 124,77 le sumás 0,01 y seguís apretando “=”, ¿qué números irán apareciendo? ¿Cuántas veces hay que sumar 0,01 para llegar a 125?
- Si queremos ir de 13,6 a 14 sumando de a 0,01, ¿cuántas veces habrá que apretar la tecla “=”? ¿Y si lo hiciéramos sumando de a 0,001?
- Siguiendo con la calculadora.
- Ahora anotamos en la calculadora el número 1,7. Queremos ir restando reiteradamente 0,1 hasta llegar a 0. ¿Cuántas veces hay que restarlo? Recordá que primero deberás resolverlo y recién luego podrás verificarlo con la calculadora.
- Si anotamos 2,45, ¿cuántas veces hay que restar 0,01 para llegar a 2? ¿Y para llegar a 0?
- Si anotamos 0,351, ¿cuántas veces habría que restar 0,001 para llegar a 0? ¿Y para llegar a 0,3?
- Si anotamos 4,206, ¿cuántas veces habría que restar 0,001 para llegar a 4? ¿Y para llegar a 4,2?
- ¿Es posible que a partir de 4,208 y restándole sucesivamente 0,01 (solamente este número) lleguemos a 4? Justifica tu respuesta.
Sistema métrico decimal
Los siguientes problemas permiten poner de manifiesto la estrecha relación entre números decimales y el sistema métrico decimal. Es importante que el docente tenga en cuenta que ambas nociones se alimentan mutuamente. Para que los alumnos puedan abordar los siguientes problemas, será necesario que tengan presentes las unidades de longitud del sistema métrico decimal.
El análisis de la escritura y la lectura de las medidas de longitud debería llevar a discutir con los niños, por ejemplo, que la expresión 4,6 metros “esconde” el hecho de que el 6 a la derecha de la coma representa en este caso 6 décimos de metros y esto equivale a 6 decímetros; o que 4,25 km corresponde a 4 kilómetros más 0,25 km, que son 2 décimos de km (es decir, 2 hm) + 5 centésimos de km (es decir, 5 dam).Resolvé los siguientes problemas:
- Si partimos una tira de un metro en 10 partes iguales, ¿cuál es, en metros, la longitud de cada parte? ¿Y en centímetros?
- Esta tira mide
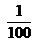de metro. Es decir que mide 0,01 metro. ¿Cuántas tiras necesitaríamos para armar una tira de 1 metro? ¿A cuántos centímetros equivale 0,01 metro? - ¿Cómo se escribe en números decimales
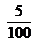de metro? - ¿Cuántos centímetros tiene una tira de
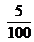de metro? Acordate que 
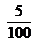de metro se escribe también 0,05 metro. - ¿A cuántos centímetros equivale una longitud de 0,5 metros? ¿Y una de 0,55 metros?
- ¿Cuántos centímetros tiene una tira de 5,5 metros?
Ya estudiaste que 
de metro es una longitud tal que 1.000 veces esa longitud equivale a un metro. 
de metro se escribe también 0,001 metro. Un milésimo de metro es un milímetro.
- ¿Cuántos milímetros tiene 1 metro? ¿Y un centímetro? ¿Qué parte de un centímetro es un milímetro?
- ¿A cuántos centímetros equivale una longitud de 0,001 metros? ¿A cuántos milímetros equivale esa misma longitud?
- ¿A cuántos centímetros equivale una longitud de 0,111 metros? (Acordate de que 0,111 es lo mismo que
)
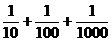Seguí resolviendo.
- ¿Qué parte de un metro son 40 centímetros?
- Completá usando números decimales: 40 cm = ……….. m
- ¿Qué parte de un metro son 123 cm?
- Completá usando números decimales: 123 cm = …….. m
- Completá la siguiente tabla que relaciona longitudes expresadas en centímetros con esas mismas longitudes expresadas en metros.
| Longitud en metros | 2,3 | 2,03 | 2,003 | 2,33 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Longitud en centímetros | 5 | 12 | 102 | 1 | 0,5 |
- ¿Qué cuenta hay que hacer para expresar en centímetros una longitud que está expresada en metros? ¿Y para expresar en metros una longitud que está en centímetros?
- Anotá todas las cuentas de multiplicar por 100 y de multiplicar por 0,01 que surgen de la tabla anterior.
- Con lo trabajado hasta ahora, respondé:
- ¿A cuántos centímetros equivalen 3 milímetros? ¿Y 30 milímetros? ¿Y 300 milímetros? ¿Y 0,3 milímetros? ¿Y 0,03 milímetros?
- Completá las siguientes tablas que relacionan longitudes expresadas en diferentes unidades:
| Longitud en centímetros | 0,4 | 0,02 | 0,42 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Longitud en milímetros | 30 | 5 | 35 | 3 | 1 | 0,5 |
| Longitud en metros | 1 | 10 | 0,1 | 0,01 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Longitud en milímetros | 1 | 10 | 100 | 111 | 0,5 |
- Una tira mide 4 metros 60 centímetros de largo. ¿Cuáles de las siguientes escrituras expresan esa cantidad?
4,060 m
460 cm
4,6 m
4 m 60 dm - Una tira mide 5 metros 8 centímetros de largo. ¿Cuáles de las siguientes escrituras expresan esa cantidad?
5,08 m
580 cm
5,8 m
5 m 8 dm - Para pasar por cierto túnel, es necesario que los vehículos tengan como máximo una altura de 2,20 metros. ¿Cuáles de los siguientes vehículos podrán pasar?
A: 207 cm
B: 2 m 30 cm
C: 2 m 1 dm
D: 2 m 10 dm
E: 2,10 m - Un automóvil recorre una distancia de 5 km 80 m y otro recorre 5,8 km. Decidí si ambos recorrieron lo mismo.
Respondé:
- ¿Cuánto es la mitad de 1 metro? ¿Y la mitad de 0,5 metros? ¿Y la mitad de 0,05 metros? ¿Y la mitad de 0,4 metros? ¿Y la mitad de 0,3 metros?
- Basándote en lo resuelto en el ítem anterior, calculá:
0,5 : 2 =
0,3 : 2 =
0,05 : 2 =
0,03 : 2 =
Resolvé los siguientes problemas:
- Si se colocan, una al lado de otra, 10 tiras de 0,5 metros de longitud cada una, ¿qué largo forman en total? ¿Cuánto es 0,5 x 10?
- Si se colocan, una al lado de la otra, 10 tiras de 0,8 metros de longitud cada una, ¿qué largo forman en total? ¿Cuánto es 0,8 x 10?
- Si se colocan, una al lado de la otra, 10 tiras de 0,04 metros de longitud cada una, ¿qué largo forman en total? ¿Cuánto es 0,04 x 10?
- Si se colocan, una al lado de la otra, 10 tiras de 0,84 metros de longitud cada una, ¿qué largo forman en total? ¿Cuánto es 0,84 x 10?
- Si se parte en 10 trozos iguales una tira de 0,5 metros de longitud, ¿cuánto mide cada trozo? ¿Cuánto es 0,5 : 10?
- Si se parte en 10 trozos iguales una tira de 0,04 metros de longitud, ¿cuánto mide cada trozo? ¿Cuánto es 0,04 : 10?
- Si se parte en 10 trozos iguales una tira de 0,54 metros de longitud, ¿cuánto mide cada trozo? ¿Cuánto es 0,54 : 10?
Comparación y orden de números decimales
- En un supermercado venden bolsas con diferentes frutas.
La bolsa A dice: “peso 3,3 kilogramos”.
La bolsa B dice: “peso 3,25 kilogramos”.
Si quiero llevar la bolsa que contiene más kilogramos de fruta, ¿cuál elijo?
- Martina pesaba 55,5 kilogramos. Hoy se subió a la balanza y extrajo un ticket que decía 55,500 kilogramos. Preocupadísima afirmaba que subió de peso. ¿Es cierto esto?
- El chocolate “Qué rico” cuesta $ 2,05 y el chocolate “Choco Choc”, $ 2,50. Los dos pesan lo mismo. ¿Cuál es el chocolate más económico?
- Completá los espacios con el signo menor (<), mayor (>) o igual (=) según corresponda:
- 1, 5 …………….. 1,50
- 0,299 …………… 0,3
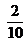…………… 0,04
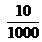…………… 0,1
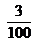…………… 0,03
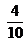…………… 0,40- Ordenar de menor a mayor: 7,4; 8,3; 7,12; 8,08; 7,04; 8,15; 8,009; 8,013
Resolvé los problemas:
- Matías y Elena jugaban a adivinar números, mientras lo hicieron con números naturales no hubo problemas, pero cuando jugaron con números decimales se generó la siguiente discusión.
MATÍAS: “Adivina, adivinador… El número que yo pensé está entre 2,4 y 2,5”.
ELENA: “Siempre el mismo tramposo, no existen números entre 2,4 y 2,5”.
¿Quién pensás que tenía razón? - Matías le dio a Elena varios ejemplos de números mayores que 2,4 y menores que 2,5. ¿Podés vos pensar algunos?
- Elena, entusiasmada, ve que ahora sí le puede ganar a Matías.
ELENA: “Adivina adivinador… Mi número está entre 1,15 y 1,16, y tiene tres cifras decimales”.
¿Qué números habrá pensado Elena? Proponé tres. - En la última jugada Matías propone: “Pensé un número que está entre 5,62 y 5,63, y tiene dos lugares después de la coma”. Elena sostiene que ganó esa mano ya que esta vez Matías sí se había equivocado. ¿Tiene razón Elena? ¿Por qué?
- Escribí tres números entre
- 1,5 y 1,6
- 2,03 y 2,04
- 5,17 y 5,2
- 11,9 y 12
- 0,2 y 0,21
- Escribí tres números decimales menores que 0,01.
- Escribí una fracción entre los siguientes números:
- 0,5 y 0,7
- 1,1 y 1,2
- 12,05 y 12,06
- Escribí un número decimal entre los siguientes números:
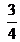y 1
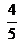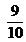
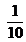y 
y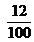 
En esta propuesta se ha presentado “un recorrido posible” para la profundización del significado de los números decimales y su relación con las fracciones. Por supuesto que las variantes y agregados quedan a cargo de cada uno de los docentes que están en las aulas.
