Dentro del núcleo estructurante Medición uno de los saberes básicos fundamentales que se ha observado tienen dificultades los alumnos es respecto al cálculo de volumen.
Este saber básico está incluido en los saberes que se proponen promover desde los Núcleos de Aprendizajes Prioritarios de séptimo grado, en Relación con la Geometría y la Medida, en donde se puntualiza:
El análisis y el uso reflexivo de distintos procedimientos para estimar y calcular medidas en situaciones problemáticas que requieran:
- calcular áreas de figuras, áreas y volúmenes de cuerpos, estimando el resultado que se espera obtener y evaluando la pertinencia de la unidad elegida para expresarlo.
- calcular volúmenes de prismas estableciendo equivalencias entre cuerpos de diferente forma mediante composiciones y descomposiciones.
A continuación se muestran algunos ítems de evaluación que obtuvieron en general menos del 50% de respuestas correctas. Por ejemplo en la evaluación de 2013 el ítem correspondiente a este saber obtuvo un 21,03% de acierto.
Los ejercicios dados corresponden a varios operativos de evaluación (provinciales, nacionales e internacionales) porque en ellos, a pesar de ser poblaciones distintas y de distintos años, los alumnos repiten los mismos errores.
Es importante recordar que cada uno de los distractores que aparecen NO han sido puestos al azar, son posibles formas de razonar que tienen los alumnos, o un aprendizaje incompleto que en algunos casos les resulta válido. Por ello en evaluación sistemática se los llama “distractores válidos”, al elegirlos queda claro el error que tienen los alumnos.
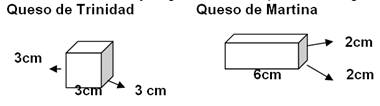
| [1]Trinidad y Martina tienen un pedazo de queso cada una. Los pedazos son de diferente forma, como muestran los dibujos. ¿Quién tiene el pedazo más grande?
|
[2]Observa el siguiente depósito de trigo. El dueño lo llena hasta la mitad. El volumen ocupado es: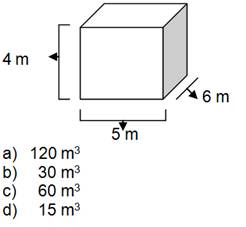 |
[3]Observa el siguiente envase de cartón.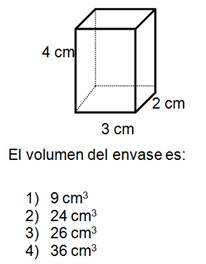 |
| [4]En una empresa necesitan embalar cajas cúbicas (que no están dibujadas), cuyas aristas miden 1m, en unos contenedores como el que muestra la figura. ¿Cuál es la cantidad máxima de cajas cúbicas que se pueden guardar en este contenedor?1) 64 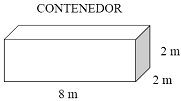 2) 32 3) 16 4) 12 |
El volumen es un tema considerado complejo y difícil de aprender para los niños y como correlato difícil de enseñar para los docentes.
Uno de los problemas en su enseñanza es tener que considerar el estudio del concepto de volumen desde dos perspectivas diferentes:
- como magnitud de medición directa (en donde se realiza el conteo del número de veces que un patrón “entra” en el volumen a medir);
¿Cuántos cubitos ![]() forman el bloque A
forman el bloque A ![]() ?
?
- como una magnitud de medición indirecta (multiplicando la medida de las tres dimensiones que componen por ejemplo un prisma).
¿Cuál es el volumen del siguiente prisma?
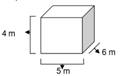
Estos dos aspectos aparecen a veces diluidos en la enseñanza, y algunas actividades apuntan a la primera perspectiva y otras a la segunda.
Esta naturaleza dual de este concepto se constituye en un obstáculo para su enseñanza.
Por otro lado, muchas veces se considera que para enseñar el concepto de volumen basta con que nuestros alumnos “apliquen fórmulas” con éxito, y si bien estos cálculos aportan al aprendizaje, no se puede reducir sólo a esto. Éste obstáculo para la enseñanza deriva de decisiones escolares, ya que la temprana introducción del lenguaje algebraico en la escuela conlleva a centrar la enseñanza en la aplicación de fórmulas, generalmente sin sentido para nuestros alumnos. Cuantas veces nos encontramos con la pregunta “Seño para calcular el área del cuadrado es lado por cuatro o lado por lado”. Es clara la tendencia de los alumnos de emplear fórmulas memorísticamente sin control sobre ellas.
Otro de los problemas de la enseñanza provienen de la confusión entre volumen y capacidad, que obviamente son magnitudes diferentes, mientras el volumen se usa para designar la característica que tienen todos los cuerpos para ocupar un espacio, la capacidad designa la cualidad de ciertos objetos (recipientes) de poder contener líquidos o materiales sueltos (arena, harina). Pero entonces donde está el problema… la capacidad de un recipiente coincide con el volumen del espacio interior delimitado por las paredes del mismo, y viceversa, el volumen de un cuerpo coincide con la capacidad de un recipiente que envolviera completamente a dicho cuerpo. Esta diferencia que para nosotros es tan obvia, no lo es para nuestros alumnos, por lo cual es necesario que sea objeto de enseñanza explícita en la escuela.
Además tanto el volumen como el área son magnitudes no lineales (como la longitud), es por ello que las medidas son más complejas y difíciles de comprender.
En el trabajo presentado por Sanmiguel Suárez (2011) el autor explica los resultados de tres ítems de evaluación relacionados con el concepto de volumen, los tipos de respuesta de los alumnos como así las dificultades observadas como resultado de las decisiones de enseñanza del concepto.
Este trabajo está completo en la bibliografía para aquellos que quieran indagar más sobre esta problemática.
En el apartado de propuestas de enseñanza, hay sugerencias y actividades para poder ir sorteando estos obstáculos.