Dentro del núcleo estructurante Medición uno de los saberes básicos fundamentales que se ha observado tienen dificultades los alumnos es respecto al establecimiento de equivalencias entre medidas.
Este saber básico está incluido en los saberes que se proponen promover desde los Núcleos de Aprendizajes Prioritarios de séptimo grado, en Relación con la Geometría y la Medida, en donde se puntualiza:
La comprensión del proceso de medir, considerando diferentes unidades y sistemas, en situaciones problemáticas que requieran:
*argumentar sobre la equivalencia de distintas expresiones para una misma cantidad, utilizando las unidades de longitud, área, volumen y capacidad del SIMELA y sus relaciones.
A continuación se muestran algunos ítems de evaluación que obtuvieron en general menos del 50% de respuestas correctas. Por ejemplo en la evaluación de 2013 el ítem correspondiente a este saber obtuvo un 48,18% de acierto.
Los ejercicios dados corresponden a varios operativos de evaluación (provinciales, nacionales e internacionales) porque en ellos, a pesar de ser poblaciones distintas y de distintos años, los alumnos repiten los mismos errores.
Es importante recordar que cada uno de los distractores que aparecen NO han sido puestos al azar, son posibles formas de razonar que tienen los alumnos, o un aprendizaje incompleto que en algunos casos les resulta válido. Por ello en evaluación sistemática se los llama “distractores válidos”, al elegirlos queda claro el error que tienen los alumnos.
| [1] Un viaje en moto a la montaña duró 40 minutos y 30 segundos. ¿Cuántos segundos duró ese viaje a la montaña?
|
[2] ¿Cuántos metros hay en 12,21 km?
|
| [3] ¿Cuántos minutos vive un insecto si muere a la semana de haber nacido?
|
[4] En 52.000 m2 hay:1) exactamente 5 hectáreas. 2) menos de 5 hectáreas. 3) más de 5 hectáreas. 4) exactamente 10 hectáreas. |
| [5] Considerando los datos de la figura, ¿cuántos centímetros más alto es Luis que María? 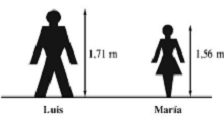
|
[6] Una bolsa con porotos colocada en un platillo de la balanza tiene un peso (masa) de 8000 gramos. 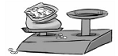 Las pesas que debo poner en el otro platillo para equilibrar la balanza son:  |
En el tratamiento escolar de la medida se suelen cometer varios errores como puntualizan algunos documentos de las provincias de Río Negro y Buenos Aires. El más destacable consiste en el apresuramiento por llegar a trabajar con los números, hecho que algunos autores llaman «la aritmetización de la medida», dejando de lado la importancia de medir. A esto colabora el uso de instrumentos «numerizados» (balanzas, relojes y cintas métricas digitales) lo cual hace que los alumnos no puedan apreciar la «materialización» de la cantidad a medir, hecho que sí se puede captar en la balanza de dos platillos al tener que equilibrar pesos con pesas visibles y sopesables; al construir el metro que servirá de unidad para medir longitudes; al analizar el reloj de manecillas que me permite una «apreciación visual» del tiempo que transcurre; entre otros.
Esta aritmetización de la medida también se vé incentivada por los docentes al pasar al rápido tratamiento del SIMELA, que si bien posee alta relevancia cultural, y un uso social indiscutido, necesita un tiempo de construcción que la escuela no se permite.
La “aritmetización” de la medida se fortalece con la insistencia sobre el tratamiento de las equivalencias en el sistema métrico. Los alumnos lo vinculan rápidamente con la regla práctica de “correr la coma”, sin controlar las relaciones entre unidades y cantidades, ni la razonabilidad del resultado obtenido. Al referirse a los errores que los alumnos cometen en las “reducciones”, Bressan y Yaksich afirman que “…muchos provienen de la falta de representaciones mentales de las unidades más comunes como referentes, lo cual les permitiría juzgar criteriosamente los resultados que logran mecánicamente”.
En este caso, dichos errores derivan de los obstáculos didácticos más que de otras causas, ya que son consecuencia lógica de las prácticas de enseñanza. Las autoras también coinciden con Chamorro (2001) en que los problemas de reducciones, de operaciones con cantidades y de reemplazo de valores en fórmulas son problemas de aritmética a través de los cuales se ejercitan operaciones con números decimales, pero que no profundizan el sentido de la medición.
Por ejemplo, ¿tienen sentido para nuestros alumnos los siguientes problemas?
- De una pieza de género se vendieron primero 0,38 hm, luego 4200 cm y por último 1 dam. Si todavía queda 1m, ¿cuántos cm tenía la pieza de género?
- Expresar en dm2 la superficie de un campo rectangular de 400 hm de largo por 500 dam de ancho que debe ser arado.
Otro aspecto que, por lo general, no se discute en las aulas es la inexactitud de la medida y el rango en que es admisible dar una respuesta cuando se trabaja con instrumentos y cuando se estima. A los niños les cuesta comprender que dos o más respuestas diferentes pueden ser igualmente valiosas a los fines de resolver un determinado problema. Los términos: alrededor de.; cerca de.; más o menos.; entre a y b., pero probablemente más cerca de.; por debajo de.; por encima de…constituyen el lenguaje de la estimación y la medida y siendo de uso cotidiano no necesitan más que ser incorporados a la vida escolar.
El apuro por iniciar al niño en el aprendizaje de las unidades legales y de reglas mecánicas de conversión entre ellas, la falta de análisis de los métodos de medir, de las unidades pertinentes de acuerdo a la precisión requerida y de los instrumentos de medición, y el empleo de un vocabulario para el tratamiento del tema, atentan realmente para una comprensión eficaz de un contenido tan relevante para la vida cotidiana, el mundo del trabajo y el quehacer en otras disciplinas.
En aconsejable que la enseñanza de las reducciones se realice con posterioridad a la comprensión de las unidades convencionales y sus relaciones.
El niño debe llegar a comprender que lo que se busca con ellas es conservar la cantidad expresándola en forma diferente, lo que equivale a usar distintas unidades para medirla.
Un principio que el alumno debe tener adquirido sólidamente previo a esta tarea es que del tamaño de la unidad depende el valor de la medida de la cantidad en cuestión. Por ejemplo, supongamos que la unidad «a» es la mitad de la unidad «b», al medir la misma cantidad (llamémosla C) con ambas unidades resultará que la medida resultante de aplicar «a» será el doble de la obtenida al aplicar «b».
Este es el criterio utilizado al «reducir» una cantidad expresada en una unidad a otra. Para ello se hace necesario establecer una compensación entre la variación de la unidad -a una más grande o más chica que la dada- y la medida obtenida de modo que la cantidad se conserve.
Ejemplos:
a) Sea expresar 3 litros en centilitros. Al utilizar cl en lugar de litros utilizo una unidad 100 veces menor que el litro (la divido por 100), luego la medida va a ser 100 veces mayor, lo que se expresa como 3l = 300cl.
b) Si en lugar de usar una unidad menor mido la misma cantidad pero con una mayor, por ejemplo kilolitros, obtendré 3l = 0,003kl, ya que siendo la unidad 1000 veces mayor que el litro (la multipliqué por 1000 en su tamaño), la medida original 3 va a quedar dividida en 1000 partes.
Es decir, que antes de comenzar a inferir las reglas mecánicas de «movimiento de la coma», es necesario hacer que el alumno comprenda la siguiente relación:
Evidentemente este proceso estará bastante allanado si los alumnos han hecho un buen trabajo con el sistema de numeración decimal donde valen las mismas reglas, pero igualmente el trabajo con éste último y con el SIMELA con simultaneidad, ocasionará beneficios mutuos de comprensión de ambos sistemas.
Es decir que el tratamiento habitual que se hace en la escuela del Sistema Métrico Decimal, impide en general a los alumnos comprender los conceptos subyacentes al mismo, y como consecuencia, éstos no disponen de medios de control sobre las conversiones habituales.
En el apartado de propuestas de enseñanza, hay sugerencias y actividades para poder ir sorteando este obstáculo.



