Los errores recurrentes evidenciados en nuestros alumnos por el bajo porcentaje de respuestas correctas en el bloque de “Operaciones” tienen sus causas en varios factores, uno de ellos es el trabajo ya más sistemático con el conjunto de los números racionales y por otro lado la incorporación del análisis de variaciones funcionales, lo que hace que los alumnos tengan que reconocer y utilizar relaciones directa e inversamente proporcionales.
Es importante remarcar que el trabajo con los números decimales y las fracciones en el segundo ciclo, implica un nuevo trabajo en la tarea docente, con la consabida complejidad que representa el aprendizaje de estos conjuntos numéricos. Se trata de un campo de contenidos complejo, cuya elaboración comienza en cuarto grado y continúa más allá de la escuela primaria, que supone rupturas importantes con las prácticas más familiares que los alumnos desplegaron a propósito de los números naturales.
Revisión del trabajo con fracciones
A continuación se presenta una serie de problemas con el propósito que los alumnos recuerden ideas vinculadas al concepto de fracción trabajadas en 4° y 5° grado.
- Resolvé los siguientes problemas:
- De un ramo de 12 flores,
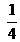son rosas. ¿Cuántas flores son rosas? - Juan le regala la mitad de sus 68 figuritas a un compañero. ¿Cuántas figuritas le regala?
- Joaquín perdió
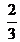de sus 30 figuritas. ¿Cuántas figuritas perdió? - En el último examen,
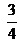de los 40 alumnos obtuvo un puntaje superior a 6. ¿Qué cantidad de alumnos tuvo esas notas? - Martín decidió regalar a su primo 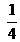de sus bolitas. Si le dio 23 bolitas a su primo, ¿cuántas tenía?
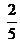de los alumnos forman parte del equipo de fútbol. Hay 32 alumnos en el equipo de fútbol, ¿cuántos alumnos hay en total?- María pegó 27 figuritas en su álbum. Si el álbum completo tiene 54 figuritas, ¿qué parte del álbum completó?
- De un ramo de 12 flores,
- Para cumplir con los pedidos del día, una confitería calcula que necesita usar 4 kg de harina. En el estante guardan 2 paquetes de 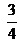kg, 2 paquetes de
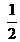kg y 2 de 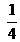kg. ¿Cómo podrías averiguar mediante un cálculo mental si la harina que tienen es suficiente? - Anotá estos números como una sola fracción:
- Anotá estas fracciones como sumas de un número entero más una fracción menor que 1:
- Decidí, sin averiguar el resultado, si es posible que
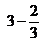dé un resultado menor que 2
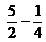sea menor que 2
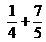sea menor que 1
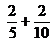sea mayor que 1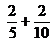- sea mayor que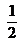
Para cada caso, pensá cómo explicar las razones de tu respuesta.En las siguientes actividades se propone recuperar las estrategias de cálculo vistas en años anteriores en relación con la suma y la resta de fracciones.
- Un corredor se entrena en una pista. Él afirma que en la primera etapa de la carrera recorrió
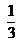de la pista, y en la segunda y última etapa recorrió los 
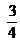restantes. ¿Es esto posible? - De una jarra que contiene 2
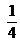litro de agua llené dos vasos de 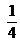litro cada uno y un vaso de 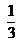de litro. ¿Cuánta agua quedó en la jarra? - A Juan le proponen que elija la bolsa de golosinas más pesada. La primera bolsa pesa 3 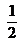kg y la segunda pesa
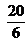kg. ¿Cuál pensás que habrá elegido Juan? ¿Cuánto pierde si elige mal? - ¿Cuánto hay que agregar a 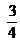para obtener
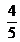? - ¿En cuánto excede
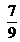a 
?
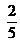Operaciones con números decimales. Suma y resta
Estos problemas están previstos trabajar para afianzar el trabajo con los número decimales.
- Lorena y Alejandra querían unir sus cintas por el borde. Lorena decía que uniendo su cinta de 1,5 metros a la de Alejandra de 1,6 metros tendrían una cinta de 2,11 metros. Alejandra pensaba que si unían ambas cintas tendrían una cinta de más de 3 metros. ¿Quién estaba en lo cierto? ¿Cómo pensó el cálculo cada una?
- En la caja del supermercado te dicen que tenés que pagar $ 5,75. Si lo hacés con un billete de $10, ¿cómo hacés para calcular mentalmente lo que te deben dar de vuelto?
- Si en el visor de la calculadora tenés el número 0,234, qué operación deberías hacer para que aparezca…
0,134 0,235 0,244 0,24 1,234
- Resolvé mentalmente
10 + 0,2 =
1 – 0,5 =
2 – 0,05 =
3 + 0,7 =
1 – 0,25 =
4 – 1,15 =
4 + 0,02 =
1 – 0,75 =
4 – 2,30 =
10 + 0,2 + 0,03 =
2 – 1,1 =
8,9 + 1,1 =
0,5 + 0,05 + 0,005 =
10 – 0,91 =
1,14 + 1,16 =
- Sumá 0,9 a cada uno de los siguientes números: 3,1; 3,11; 4,25; 0,73; 2,99.
Restá 0,9 a cada uno de los siguientes números: 8,6; 3,4; 12,5; 8,25.
Sumá 0,09 a cada uno de los siguientes números: 2,23; 1,75; 9,91; 3,55.
Restá 0,09 a cada uno de los siguientes números: 8,29; 12,71; 4,35; 8,28.
- Algunas personas cuando tienen que sumar 0,9 a un número decimal le suman 1 y luego le quitan 0,1. Por ejemplo, para hacer 3,4 + 0,9, lo piensan así: 3,4 + 1 = 4,4. Luego hacen 4,4 – 0,1 = 4,3. Entonces 3,4 + 0,9 = 4,3. Esta regla funciona. Teniendo en cuenta los cálculos que realizaron en el ejercicio anterior, ¿qué reglas escribirán para restar 0,9? ¿Y para restar 0,09? ¿Y para sumar 0,09?
- Calculá mentalmente:
35,15 + 0,19 =
2,134 + 0,199 =
8,34 – 1,9 =
15,60 + 1,99 =
9,53 – 2,9 =
7,931 + 2,99 =
- Matías y Diego jugaban a “Quien no pasa la línea”. Matías partía del 0 y siempre debía sumar un número. Diego partía del 1 y siempre debía restar un número. Matías no podía llegar a un número mayor que el de Diego; de lo contrario, perdía. Diego no podía llegar a un número menor que el de Matías, pues, de lo contrario, perdía él.
Estas son las primeras jugadas:
Matías Diego 0 1 +0,1= -0,1= +0,1= -0,1= +0,02= -0,1= +0,005= -0,05= +0,0005= -0,09= ¿A qué número llegó cada uno de los participantes? ¿Puede Matías agregar 3 números más sin perder? ¿Y Diego?
Multiplicación y división de una fracción por un número natural
Las relaciones de proporcionalidad directa constituyen un ámbito a partir del cual repensar aspectos sobre el funcionamiento de las fracciones. En particular brindan un contexto en el que apoyarse para resolver operaciones de multiplicación y división de fracciones por números naturales (y de números naturales por fracciones).
Para abordar estos problemas es conveniente que los alumnos puedan partir de la siguiente idea: en una relación de proporcionalidad directa se cumple que al doble de una cierta cantidad le corresponde el doble del correspondiente de dicha cantidad, al triple le corresponde el triple y, en general, cuando una de las cantidades se multiplica o divide por un número, la cantidad correspondiente se multiplica o divide por el mismo número. Es claro que no se espera esta formulación por parte de los alumnos pero sí se requerirá que sean capaces de poner en juego estas relaciones.
Los siguientes problemas apuntan a que los alumnos traten la multiplicación y la división de fracciones por un número natural, apoyados en contextos que favorecen la puesta en juego –seguramente implícita– de propiedades de la proporcionalidad directa.
- Completá las siguientes tablas:
Tabla 1
Esta tabla relaciona la cantidad de leche necesaria para la receta de un flan, según la cantidad de porciones que se desea obtener. Para esta receta se calcula litro de leche para 3 porciones.
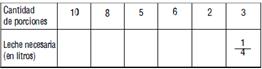
Tabla 2
Esta tabla relaciona la cantidad de personas invitadas a un asado con la cantidad de carne que habrá que comprar. Para el asado se calcula kg de carne cada 3 personas.
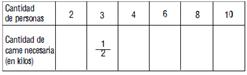
Tabla 3
En otro asado, calculan kg de carne cada 3 personas.
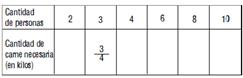
Tabla 4
La siguiente tabla relaciona la distancia que recorre un robot de juguete según la cantidad de pasos que da. El robot da pasos de 
de centímetro.
- Dos amigos discuten acerca de la cantidad de achuras necesarias para 6 personas sabiendo que se calculan 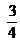kg cada 4 personas.
El primero piensa lo siguiente:
• La mitad de es 
, por lo tanto, para 6 personas hacen falta 
o 
.
La otra piensa así:
• La mitad de es y la mitad de es 
. Eso es lo que necesito por persona, entonces para 6 personas necesito 
.
¿Son correctos ambos procedimientos? ¿Cómo justificás tu afirmación?
- Laura, Aníbal y Julieta se pusieron de acuerdo: al terminar la fiesta dividirían el resto de la torta en tres partes iguales, una para cada uno. Completá la siguiente tabla que relaciona la fracción de torta que recibirá cada uno, según la cantidad de torta que sobró en la fiesta:
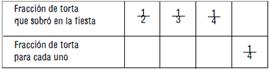
- La siguiente tabla es parecida a la anterior, pero en este caso no se sabe entre cuántos amigos se repartió la torta que sobró. ¿Podés averiguarlo?
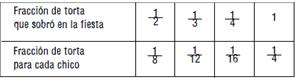
- Ahora armá una tabla como la anterior en la que la torta que sobra se reparte entre 5 amigos. Tenés que decidir qué números pondrás en la tabla. Seguramente tus compañeros no decidan incluir los mismos números que vos; eso no significa que las tablas estén mal.
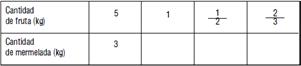
- En la siguiente tabla se muestra la relación entre cantidad de fruta que se usa para hacer mermelada y la cantidad de mermelada que efectivamente se obtiene. Completala.
Multiplicación de fracciones. Inverso multiplicativo
Se plantean actividades, en donde los alumnos pondrán en juego la noción de inverso multiplicativo: números cuyo producto es 1. Se propone esta cuestión en el contexto de áreas de rectángulos y luego se plantea un trabajo numérico descontextualizado. La aceptación que, en el conjunto de los números racionales, se puede “pasar” multiplicando de un número racional cualquiera a otro cualquiera es compleja, porque rompe con una concepción muy sólida de los alumnos, apoyada en sus conocimientos sobre números naturales, según la cual, para pasar de un número a otro multiplicando, es necesario que el segundo sea múltiplo del primero. La noción de “múltiplo” pierde sentido en el conjunto de los números racionales porque cualquier número podría ser múltiplo de cualquier otro.
- Resuelve los siguientes problemas:
- Un rectángulo tiene un m2 de área. Si su base mide 2 m ¿Cuánto mide su altura?
- Un rectángulo tiene un m2 de área. Si su base mide 4 m ¿Cuánto mide su altura?
- Ahora vamos a considerar un rectángulo tiene 2 m2 de área. Si la base mide 4 m ¿Cuánto tiene la altura?
- ¿Cuántos rectángulos posibles hay que tengan 1 m2 de área? Halla pares de valores que puedan ser base y altura de dichos rectángulos.
(Sugerencia para el docente: se puede cambiar por cm o cuadraditos de la carpeta, y pedirle a los alumnos que los dibujen).
- Ya sabés que el área de un rectángulo se calcula multiplicando la longitud de la base por la longitud de la altura. Esto significa que, del problema anterior, se pueden “extraer” multiplicaciones que dan 1. Anotalas y discutí con tu compañero si él anotó las mismas.
- Completar los siguientes espacios en blanco:
5 x……= 1
x…..= 2
6 x……= 1 8 x…..= 2
x…..= 1 7 x……= 2
x…..= 1
- Más problemas con rectángulos.
- Ahora vamos a trabajar sobre rectángulos cuya área es 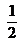m2. Si la base mide 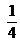m, ¿cuánto mide la altura? ¿Y si la base mide 4 m? ¿Y si la base mide 3 m?
- Completá la siguiente tabla en la que se relacionan la base y la altura de un rectángulo cuya área es de 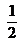m2
- Ahora vamos a trabajar sobre rectángulos cuya área es
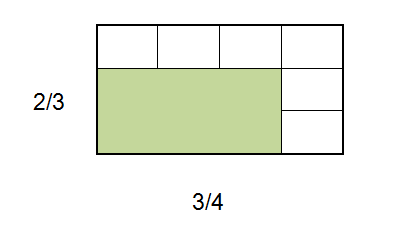
- Una parte de un terreno rectangular se destinará a la construcción de una escuela. El sector destinado a la construcción tendrá
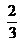del ancho y 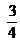del largo del terreno. ¿Cuál será la superficie que ocupará la escuela si se toma como unidad de medida el área de todo el terreno?
¿Qué parte del lote ocuparía la escuela si se le asignara 3/5 del largo y 1/2 de ancho del terreno?
- ¿Cuál de los siguientes cálculos permite averiguar que parte del rectángulo está pintado de azul?
a) 
b) 
c) 3 x 2 d) 
- Escribe una división de fracciones en la que se obtenga 1 como cociente.
- Completa los siguientes espacios en blanco:
a.
b.x….= 1 entonces 1:
c.
d.e.
f.g.
h.
- Sin hacer ninguna cuenta selecciona la opción que consideres correcta.
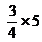menor/mayor/igual que 5
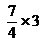menor/mayor/igual que 3
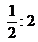menor/mayor/igual que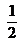
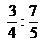menor/mayor/igual que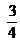
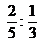menor/mayor/igual que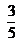 
- Mariano y Romina, discutieron lo siguiente:
Romina: “No hay un número natural que multiplicado por 3 de 2”.
Mariano: “Sí, puedo encontrar un número. Es más, si me dan dos números enteros, siempre puedo encontrar otro número racional que multiplicado por el primero me de el segundo número”.
¿Qué te parece lo que discutieron? ¿Quién tiene razón? ¿Estás de acuerdo con lo que dice Mariano? ¿Por qué?
